Study on Erasure Coding Technology Spectrum
Summary of study, also put to respective WeiChat articles.
Besides Reed-Solomon (RS) codes and regenerating codes, there are many types of codes and optimizations. Here we summarize the erasure coding (EC) technology spectrum.
Coding Techniques for Repairability in Networked DistributedStorage Systems by F.Oggier is great material that covers coding theory basics and spectrum of coding features beyond plain RS code (see chapter 5):
- 1) Reduce network traffic
- 2) Reduce number of nodes contacted
- 3) Reduce disk IO amount
- 4) Repair multiple failures at once
- 5) Distribute repair loads and parallize repair process
- 6) Reduce the time to complate repairs
Guidance as they are, actual codes may optimize one or more aspects. Besides the above, Erasure Codes for Storage Systems - A Brief Primer by J.Plank also gives good summary.
For category (5), Ceph distributes PG across OSDs, so the recovery workloads are distributed across the cluster; this is almost a standard method in cloud storage, and what the old RAID is learning from; also, faster repair means less exposure time and higher MTTF.
Regenerating Codes
I have dedicated blog Study on Regenerating Code previously.
Regenerating codes target on categorize (1). Saving over 50% network bandwidth though, they usually need to contact more nodes, thus more network IO counts, won’t reduce disk IO. Usually they can only repair 1 failure at once. While RS codes, though more network traffic, can do repair multiple and replicate to reduce network bandwidth too. Cloud storage, however, may seek for codes with less IO rather than less network storage.
Classic papers are Network Coding for Distributed Storage Systems, which firstly proposed regenerating code and MBR/MSR point. It uses information flow graph to theoretically calculate lower bounds of network traffic.
Optimal Exact-Regenerating Codes for Distributed Storage at the MSR and MBR Points via a Product-Matrix Construction constructs MBR and MSR codes achieving the lower bounds of network traffic. MBR introduces more storage overhead, while MSR applies only to codes of ~2x storage overhea, and introduces more computational overhead.
Explicit Constructions of High-Rate MDS Array Codes With Optimal Repair Bandwidth uses array code to construct a simpler and less computational expensive regenerating code. But when the code is longer, i.e. have more fragments, the array length grows exponentially beyond practical.
Update 20180305: Clay Codes is a significant work that is 1) MSR regenerating code 2) Allows n<2k-2 or small d, i.e. low storage overhead 3) Able to repair multi-node failure with reduced traffic 4) Vector code with small sub-packetization level. These solved almost every problem of regenerating code, which previously hanging around for years. Clay Code proposed the first practical MSR code for production.
Locally Redundant Codes (LRC)
LRC code family is used in Azure Storage and patented by MS. Erasure Coding in Windows Azure Storage has more details. The locality of codes have more history.
There is continous effort in MSR to seek for codes with less recovery IO and no storage bloat. In early times Rethinking Erasure Codes for Cloud File Systems: Minimizing I/O for Recovery and Degraded Reads uses pre-calculated recovery scheduling to find which path needs least fragments to reconstruct failed fragments. It also proposed rotated RS code, in which user read blocks are more likely to overlap with blocks read for reconstruct reads, so that less data need to be read. Pyramid Codes reference it as 20%-30% IO reduction, but LRC does even better.
The basic idea of Pyramid Codes: Flexible Schemes to Trade Space for Access Efficiency in Reliable Data Storage Systems is to break one parity fragment into two, each covering a local range of data fragments. The generalized pyramid codes allow parity fragments to cover any locality range they want, they may overlap, and they should have coding matrix that achieves optimal recovery, i.e. able to recover any failure combination in theory. It also gives an interesting method to construct the optimal recovery matrix by utilizing nullspace vector. LRC is Pyramid Codes.
On the Locality of Codeword Symbols analyzes the theory lower bounds of locality r with extensive math. Given hamming distance d (i.e. recoverable for any d-1 failures), and don’t bloat more storage overhead than RS code, we have: n − k >= roof(k/r) + d - 2. LRC reaches that lower bound. This paper, together with Simple regenerating codes: Network coding for cloud storage and Self-repairing Homomorphic Codes for Distributed Storage Systems, are considered to firstly proposed “locality”, which turns out to be a good characteristic in codes.
The power of Pyramid Codes is that the methodoloy applies to not only RS codes, but also any type of codes, such as XOR codes. Also, the existing optimization methods for RS codes can be applied to Pyramid Codes too. Optimizing Cauchy Reed-Solomon Codes for Fault-Tolerant Storage Applications is important for optimizing RS codes computation
- Use cauchy matrix instead of vandermonde matrix as the coding matrix. So that, we can map GF(2^w) to GF(2). The expensive multiplication on GF(2^w) becomes cheap XOR on GF(2).
- The coding matrix including less 1’s, corresponds to less XOR when encoding, i.e. less computational overhead
- Vector operations in Intel CPU, the SSE/AVX instruction set, have greatly improved coding performance.
Besides, there are other interesting optimizations, such as Optimizing Galois Field Arithmetic for Diverse Processor Architectures and Applications. This paper maps big GF(2^w) into several smaller GF(2^w’), so that multiplication lookup table is smaller. The lookup table is also optimized. And smaller table can be pinned in cache, which is important for performance. Also, application-specific customizations can improve performance further. These methods are used in Jerasure: A Library in C/C++ Facilitating Erasure Coding for Storage Applications, which is an opensource EC library first published by J.Plank.
Locally Repairable Codes is also trying to determine the theory lower bound of locality r. Different from On the Locality of Codeword Symbols, it allows relaxing storage overhead. Each node stores a=(1+e)M/k data. The locality lower bound becomes: d<=n-roof(k/(1+e))-roof(k/(r(1+e)))+2. The example constructs it gives is right the Simple Regenerating Code. The code needs 1/3 extra storage space than RS code, but it is super simple, tolerates as many failures as RS, only needs to contact 4 nodes for recovery no matter total node count, only needs to transfer 2/3 of each node data, and only needs XOR for recovery unless too many nodes are lost. Facebook datacenter was experimenting XORing Elephants: Novel Erasure Codes for Big Data on Hadoop, which is another well-known adoption of “Locally Repairable Codes”.
The third locality paper is Self-repairing Homomorphic Codes for Distributed Storage Systems by F.Oggier. It constructs code by a series of interesting polynominal transforms. The p(a+b)=p(a)+p(b) allows two parities to recover another one, with only XOR, and with the minimum locality. The code itself is not MDS, nor systematic.
XOR-based Codes
A big branch of codes is the codes that only use XOR. RS codes have the best fault tolerance against storage overhead, but it requires arithmetic multiplication on galois field. Compared to XOR, i.e. galois add, mul is much slower. XOR-based codes are usually fast at encoding and recovery, contacts less nodes; but usually they are only able to recover 2 or 3 failures, or they require extra storage overhead to tolerate more. This is because we only use XOR to construct codes.
XOR codes usually have many different path to recover the same set of failures, thus recovery scheduling / recovery equations / optimal recovery are necessary.
Generally, XOR-based codes are vastly used for RAID; while RS-based codes are widely used by cloud storage. Cloud storage requires better recoverability for multi-disk/node failures, and is more sensitive to cost due to storage overhead.
EVENODD: An Efficient Scheme for Tolerating Double Disk Failures in RAID Architectures is one of the earliest XOR codes, and very famous. It has n data disks and 2 parity disks. One encodes the horizontal strips, and one for diagonal. It tolerates 2 disk failures, achieves MDS, and has good encoding and recovery performance. Later, there is recovery scheduling improvement on EVENODD, Rebuilding for Array Codes in Distributed Storage Systems.
X-Code: MDS Array Codes with Optimal Encoding is an elegant code that , different from EVENODD, encodes the two diagonals. It is also MDS and tolerates 2 failures.
STAR: An Efficient Coding Scheme for Correcting Triple Storage Node Failures adds the third parity, that encodes the other diagonal than EVENODD, to tolerate 3 disk failures.
RDP (row-diagonal parity) code is a popular code. It is of n+2, one parity encodes horizontal strips, and one for diagonal (slightly different from EVENODD). It tolerates 2 disk failure. Optimal Recovery of Single Disk Failure in RDP Code Storage Systems proposed the optimal recovery scheduling, which achieves mimimum disk IO count and balanced recovery workload across disks. Besides, EMC XTremIO uses XDP, which is similar to RDP.
Flat XOR-based erasure codes in storage systems: Constructions, efficient recovery, and tradeoffs is another classic code. LDPC codes (talk later) only outperforms RS code after fragment (i.e. symbol) count >= 50; it is designed for large codes; and the characteristics are only stable for large codes. Flat XOR is like a “small” LDPC, which needs less fragments (5~30) to work well, and whose characteristics can be analyzed clearly in math. It sacrifices some storage space, tolerates 2-3 failures, contacts less nodes and yields much better recovery performance than RS codes.
LDPC (Low-density parity check) codes are very famous and extensively researched. It is widely used in communication, able to recover many failures (i.e. lossy channel). It is used in 10GBase-T Ethernet and Wi-Fi 802.11 standards (wiki). However, LDPC is designed for large codes. It only outperforms RS code after fragment count >= 50. The characteristics analysis are asymptotic, i.e. only for large codes can we know its properties clearly. Due to these, LDPC is rarely used in storage systems, not like in communication. LDPC can be represented as bipartite graph; data fragments are on the left, and parities on the right. An edge from left to right means to XOR the data to parity. The edges are generated randomly from given in/out degree distributions. The code generator matrix is a low-density matrix with only 1’s in it. A Practical Analysis of Low-Density Parity-Check Erasure Codes for Wide-Area Storage Applications is a good paper that compares 80+ published LDPC codes, very useful to get to know LDPC.
The RAID-6 Liber8tion Codes is a famous code used in RAID6. It performs well, uses only XOR, achieves MDS, and has minimum 1’s in coding matrix. In some scenarios, it outperforms RDP. The paper also optimized the recovery scheduling for Liber8tion codes. Besides, the paper is a good summary for all other types of XOR codes in RAID.
Calculating MTTF
Fragment lost status transition is usually modeled as Markov state transition model. The MTTF can be calculated by standard methods in “Adventures in stochastic processes”. Some papers are telling how and why. A better material is the cat and mouse example. I will follow this example
Question 1: We know the survival probability of each steps (or call it rounds) in the markov model. How do we calculate MTTF?
- Markov model transit step by step. In each step we can calculate the probability of survival. It can be drawed as the graph on the left.
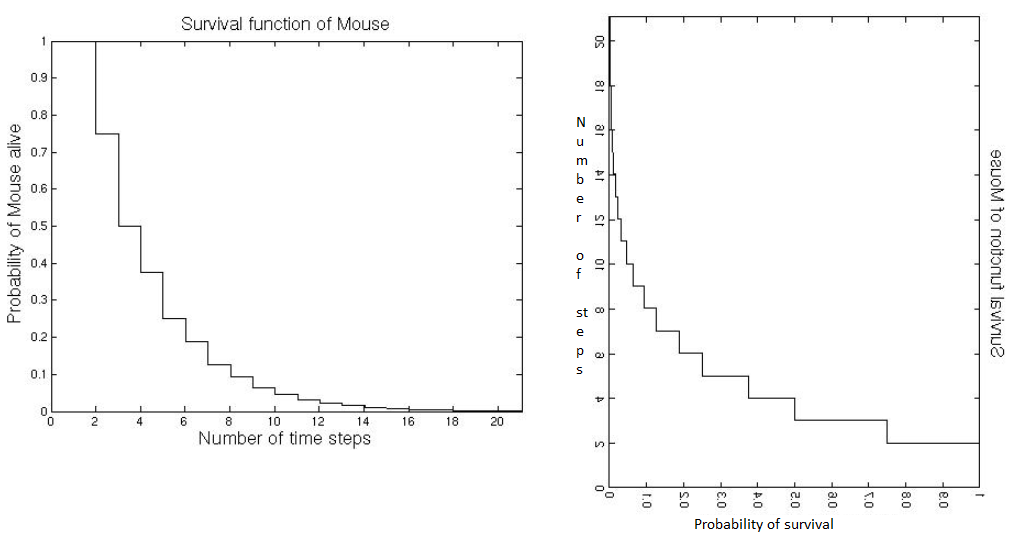
- Suppose we know the graph already, how do we get the MTTF? MTTF is can be seen the probability average of steps. Flip the graph on the left by the y=x axis, you get the graph on the right. It is the probablity distribution of number of steps. So, the average value of steps, i.e. MTTF. equals to the area. MTTF = sum up the survival probability of each step.
Question 2: How to calculate the survival probability at step n?
- Non-survival means we are staying at stationary states, or call it absorbing states. Survival means we are staying at non-stationary states. The probability of survival is to add the probabilities of each non-stationary state up.

Question 3: How to calculate the MTTF?
- Since we have the survival probability at step n already. In the last step of the above picture, MTTF is calculated. When we are using “steps”, the MTTF is the in unit of “steps”. If we are using failure probability per hour, the MTTF becomes expected hours of survival, which is commonly used in EC storage.
Question 4: How come the (I + T + T^2 + T^3 + ...) = (I - T)^(-1)?
- Multiply
(I-T)to both right sides of the equation. You will getlim(n->+∞):(I - T^(n+1)) = I. Since theTabove is for non-stationary states,T^nwill eventally trend to zero, because all states eventally escape to stationary (i.e. failure). We have the above question proved.
As in Availability in Globally Distributed Storage Systems, EC for cloud storage is to improve reliability in the constraint of cost. The paper gives extensive content, including various comparisons, data, and how to calculate MTTF. More importantly, this paper put emphasis on correlated failures, which is the true MTTF killer in cloud storage. Multi-site is also discussed; it is a method to break the chain of correlated failures. There are other papers analyzing the MTTF too and what are the keys to cloud storage reliability and cost. See paper notes.
Paper notes
Raw paper reading notes. There are more contents here. Not all are covered above.
1. readings: write notes for papers read
---- Misc papers ----
1. Malacology: A Programmable Storage System [2017, 0 refs (not published yet)]
https://www.soe.ucsc.edu/sites/default/files/technical-reports/UCSC-SOE-17-04.pdf
1. Initially Ceph invented the dynamic subtree partitioning to manage CephFS metadata
Dynamic Metadata Management for Petabyte-scale File Systems
http://ceph.com/wp-content/uploads/2016/08/weil-mds-sc04.pdf
After CephFS implementation ready, authors found allowing endusers to customize metadata partition/migration/balancing strategy is necessary. Thus Mantle API came out
Mantle: A Programmable Metadata Load Balancer for the Ceph File System
https://www.soe.ucsc.edu/sites/default/files/technical-reports/UCSC-SOE-15-10.pdf
Now, in this paper, authors combine all Ceph originated enduser customizable APIs, as Malacology, the programmable stoage system. Also, the ZLog stuff is put in
Interesting paper. Worth read
2. Highlights
1. Service Metadata Interface: the MON paxos is exposed as API
Data I/O Interface: Ceph originally has the dynamic object interface by Lua
Distributed Metadata Interface: CephFS metadata allows policies
File Type Interface: Allows customize inode types
Load Balancing Interface: CephFS metadata load balancing allows policies; policies can be stored in MON or OSD
Durability Interface: Ceph OSD
2. Services built on Malacology
Mantle: Programmbale load balancer for CephFS metadata. policies are stored in MON or OSD. use Lua to program
ZLog: A fast distributed shared log. sequencer uses File Type interface, to make itself a shared file
the sequencer implementation is interesting and crucial for ZLog performance
---- Coding theory ----
2. Optimizing Cauchy Reed-Solomon Codes for Fault-Tolerant Storage Applications [2006, 208 refs]
http://web.eecs.utk.edu/~plank/plank/papers/CS-05-569.pdf
1. very good paper. after all these EC code study, though there are many fancy ones,
RS code (or those based on RS code) is still the most suitable one for practical use.
this paper gives the important computational optimization for RS code encoding/decoding
2. highlights
1. many codes use only XOR, this is fast, but won't achieve best recoverability against storage overhead.
RS code needs galois multiplication more than XOR.
2. how RS code get fast to compute today
1. Intel SSE/AVX instructions (vector instruction sets) allow GF (galois field) multiply operations to be much faster
Erasure Codes for Storage Systems A Brief Primer: http://web.eecs.utk.edu/~plank/plank/papers/Login-2013.pdf
1. there are techniques such as make all matrix coefficients as power of 2 (Linux RAID-6)
2. CRS code - Cauchy Reed Solomon code use Cauchy matrix instead of Vandermonde maxtrix
1. with CRS, word size w can be selected as small as possible, rather than limited by 4, 8, 16
2. ((n + m) * n) cauchy code matrix, all n*n submatrices may be inverted in O(n^2) GF operations [Rab89]
3. use projects to covert operations over GF into XORs. this is genius. see paper for graphic illustration
1. every element e in GF(2^w) can be represented by a 1 × w column vector of bits, V (e), or a w × w matrix of bits, M(e)
2. the i-th column of M(e) is equal to the column vector V (e^(2^(i−1)))
3. M(e1) * V (e2) = V (e1e2), M(e1) * M(e2) = M(e1e2)
4. So, GF(2^w) is projected onto GF(2), where multiply is also XOR.
the computation now take place on plain bits, so w doesn't need to be multiply of 8
and, the number of 1's in cauchy matrix corresponds to XOR count
4.5. encoding: O(nlog(n+m)), decoding O(n^2)
5. another material: 基于柯西矩阵的Erasure Code技术详解
http://alanwu.blog.51cto.com/3652632/1410132
4. Cauchy with less 1's has less XOR count in encoding
So, find optimal cauchy matrix with minimal 1's after projected to GF(2)
1. some general experience: larger w has more 1's in general. small w is favorable
(but there are some exceptions, detail in paper)
2. the author spent much effort on enumerating matrices to find optimal ones with different (n, m, w)
3. related materials
1. Optimizing Galois Field Arithmetic for Diverse Processor Architectures and Applications
http://www.kaymgee.com/Kevin_Greenan/Publications_files/greenan-mascots08.pdf
1. multiplication requires a variety of implementation techniques that depend on hardware, memory, co-processing elements and word size w
3. Coding Techniques for Repairability in Networked Distributed Storage Systems (Fr´ed´erique Oggier)
http://phdopen.mimuw.edu.pl/lato12/longsurvey.pdf
1. very good reading. this part I start to read Part II to end of paper.
this paper here provides the general framework of what categories of EC codes we have
2. highlights
1. beyond of RS code. there are many directions of current EC code study
(another paper has similar summary is: Erasure Codes for Storage Systems A Brief Primer
http://web.eecs.utk.edu/~plank/plank/papers/Login-2013.pdf)
1. reduction in overall data transfer over the network
1. the example is regenerating codes. they reduce total network traffic,
but likely to increase number of network IOs, and usually cannot repair multiple faults
2. reduction in the number of nodes contacted, i.e. repair fan-in
1. Simple regenerating codes, Flat XOR codes
3. reduction in the amount of data that needs to be read from the live nodes, i.e. disk I/O
1. RDP codes
4. possibility to repair multiple faults
1. LDPC codes can do it. and RS based codes, such as LRC. and some specially designed regenerating codes.
5. possibility to distribute the repair load and parallelize the repair process and
1. Ceph PG scattered around OSDs
6. reduction in the time to complete repairs
1. first, it is Codes on Codes. a simple example "Product Codes"
2. next Hierarchical Codes [11], Pyramid Codes [19] and Local Reconstruction Codes [18], they two are famous
3. others, Cross-object Coding
4. Locally Repairable Codes
1. Self-Repairing Codes (most paper published by this author F. Oggier)
2. Punctured Reed-Mueller Codes
2. Besides, we have many XOR based codes: LDPC code, RDP code, Flat-XOR codes, X-Code, etc
4. Optimal Recovery of Single Disk Failure in RDP Code Storage Systems [2010, 98 refs]
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.439.9023&rep=rep1&type=pdf
1. RAID-6 uses double XOR parities. The clever way is one parity for row and another for diagonal, i.e. RDP.
RDP tolerates 2 disk failures at most. RDP uses only XOR operation. RDP needs n+2 storage overhead.
This paper RDOR improves how to recover with 1 disk failure. It uses two parties together,
and the algorithm achieves minimal disk read IO, and balance read against all disks.
there is extensive math analysis to find the optimal disk reads and load balance point.
2. RDP is a very classic XOR based code, besides this paper, there are many improvements on it.
It is frequently used in RAID.
3. EMC XtremIO is using XDP, which is similar to RDP.
https://www.emc.com/collateral/white-paper/h13036-wp-xtremio-data-protection.pdf
5. Flat XOR-based erasure codes in storage systems: Constructions, efficient recovery, and tradeoffs [2010, 74 refs]
https://pdfs.semanticscholar.org/09be/d5a75cbdba4b930cdca6bd2499d61121e030.pdf
1. If you want a "small" LDPC code, that's Flat XOR. It is a much faster code than RS/MDS codes, with bigger storage overhead compared to recoverability
Generally, the storage overhead is ~1.5, tolerage fragment falure is 2~3, recovery fan-in is ~5-10, read load can be ~0.2-0.5
this papers propose the code construction and recovery schedule methods.
but compared to usually used MDS code, flat XOR needs k=5 to 30, this is still relatively long. long codes are bigger probability to fail for all fragments
2. related works
1. compared to LRC code, LRC uses less storage overhead, when provide similar or smaller local recovery cost
https://www.microsoft.com/en-us/research/wp-content/uploads/2016/02/LRC12-cheng20webpage.pdf
6. X-Code: MDS Array Codes with Optimal Encoding [1999, 354 refs]
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.30.9205&rep=rep1&type=pdf
1. It's array code, the 2 parity row it attached at bottom. Each parity encodes left or right diagonal with only XOR. So, it looks like a big X.
the update is optimal, with complexity 2. the code recovers at most 2 failures, with n+2 storage overhead, it's MDS.
2. thinkings
1. the optimal update complexity 2 is not uncommon. this is by nature for array code.
if not array code, e.g. just plain RS, we can use 2 parities, and each encode packet is small.
the update complexity is the same, i.e. 2 parity packets
7. LDPC Codes: An Introduction
https://www.ics.uci.edu/~welling/teaching/ICS279/LPCD.pdf
1. LDPC codes usually have many data/parity fragments, i.e. the code is large. Parities only use XOR. Each parity covers some data fragments.
The code matrix is a sparse matrix containing only 1's. LDPC can be ~2 storage overhead, low computation cost, and able to recover from large amount of fragment erasures.
The code matrix can even be randomly generated. Using iterative belief propagation techniques, LDPC codes can be decoded in time linear to their block length
There are extensive researches on LDPC. LDPC code is rarely used in storage, but much in network communication (10GBase-T Ethernet, Wi-Fi 802.11)
2. other LDPC introductions
1. Low-density parity-check code
https://en.wikipedia.org/wiki/Low-density_parity-check_code
https://zh.wikipedia.org/wiki/%E4%BD%8E%E5%AF%86%E5%BA%A6%E5%A5%87%E5%81%B6%E6%AA%A2%E6%9F%A5%E7%A2%BC
2. Introduction to LDPC Codes
http://circuit.ucsd.edu/~yhk/ece154c-spr15/ErrorCorrectionIII.pdf
3. A Practical Analysis of Low-Density Parity-Check Erasure Codes for Wide-Area Storage Applications
http://loci.cs.utk.edu/lors/files/DSN-2004.pdf
3. some comments
1. "When the ratio of networking performance to CPU speed is high enough, LDPC codes outperform their MDS alternatives.
However, when that ratio is lower, MDS codes perform better [PT04, CP05]."
-- [Optimizing Cauchy Reed-Solomon Codes for Fault-Tolerant Storage Applications](http://web.eecs.utk.edu/~plank/plank/papers/CS-05-569.pdf)
2. "LDPC ... had a significant impact in networked and communication systems ... The appeal of LDPC is that, for large such codes,
a small amount of space-efficiency can be sacrificed to significantly reduce the computation costs required to encode and decode data over lossy channels"
-- [Flat XOR-based erasure codes in storage systems: Constructions, efficient recovery, and tradeoffs](https://pdfs.semanticscholar.org/09be/d5a75cbdba4b930cdca6bd2499d61121e030.pdf)
8. Pyramid Codes: Flexible Schemes to Trade Space for Access Efficiency in Reliable Data Storage Systems [2007, 283 refs]
https://staff.ie.cuhk.edu.hk/~mhchen/papers/nca.07.pyramid.codes.pdf
1. good paper. one of the founding paper of locality codes. basic pyramid code is to break a parity in RS code into two, each covering half of data fragments
generalized pyramid code has parities each cover a group of data fragments, groups may overlap, and code matrix should achieve "Maximally Recoverable"
the paper also gives an interesting algorithm to construct optimal matrix, by using null space vector, see III.C.3.
Besides, the pyramid code can be applied in other code, including those XOR codes, such as RDP, X-Code, EVENODD, B-Code, CPM
It can also be optimized by the Cauchy Reed-Solomon code optimization techniques
2. founding papers of locality codes
1. "Code locality was identified as a good metric for repair cost independently by Gopalan et al. [14], Oggier et al. [6], and Papailiopoulos et al. [15]"
---- as in [Locally Repairable Codes](http://www-scf.usc.edu/~papailio/repair_locality_ISIT_short.pdf)
[14] P. Gopalan, C. Huang, H. Simitci, and S. Yekhanin, “On the Locality of Codeword Symbols,” Preprint available at http://arxiv.org/abs/1106.3625.
[6] F. Oggier and A. Datta, “Self-repairing homomorphic codes for distributed storage systems,” in Proc. IEEE Infocom 2011, Shanghai, China, Apr. 2011.
[15] D. S. Papailiopoulos, Jianqiang Luo, Alexandros G. Dimakis, C. Huang, and J. Li,
“Simple Regenerating Codes: Network Coding for Cloud Storage”, accepted in IEEE International Conference on Computer Communications (Infocom) 2012, Miniconference
3. related papers
1. On the Locality of Codeword Symbols
https://arxiv.org/abs/1106.3625
1. gives the math analysis of lower/upper bounds of locality with other codec parameters, such as
disk/network IO count, transmitted bandwidth, recoverability, update cost, storage overhead, etc
2. Erasure Coding in Windows Azure Storage
https://www.usenix.org/system/files/conference/atc12/atc12-final181_0.pdf
1. this paper proposed the LRC code used in Azure. it is a generalized pyramid code
3. algorithm to construct optimal coding matrix
1. the algorithm finds the next row one by one. each row needs to be linear independent with previous each (n-1) row selection, i.e. the recovery submatrix
2. for each recovery submatrix, find the null space vector uj, then next_row * uj != 0 is required. if it == 0,
make next_row <- next_row + e * uj. this guarantees next_row * uj != 0.
3. to maintain the previous each recovery submatrix still have the != 0 property, we filter out bad e's.
a bad e is the e to make ui * (next_row + e * uj) == 0
9. On the Locality of Codeword Symbols [2011, 328 refs]
https://arxiv.org/pdf/1106.3625.pdf
1. this paper analysis with extensive math the locality tight lower/upper bounds for parity codes against hamming distance d recoverability and a broad class of parameter settings
it outlines the complete picture of the tradeoffs between codewords length, worst-case distance and locality of information symbols
interesting paper to read. need to fully understand the math. key conclusion: n − k >= roof(k/r) + d - 2, and equality can be achieved (Canonical Codes).
---- Reliability in storage ----
10. Availability in Globally Distributed Storage Systems [2010, 387 refs]
https://www.usenix.org/legacy/event/osdi10/tech/full_papers/Ford.pdf
1. Good paper. based on 1-year study in Google on live operations. it reveals the importance of modeling correlated failures when predicting availability.
and introduced multi-cell replication schemes in the reliablity Markov model. Findings show correlated failure makes recovery rate ineffective to improve MTTF.
2. highlights
1. works done in google
1. Compare mean time to failure for system components at different granularities, including disks, machines and racks of machines. (Section 3)
2. Classify the failure causes for storage nodes, their characteristics and contribution to overall unavailability. (Section 3)
3. Apply a clustering heuristic for grouping failures which occurs almost simultaneously and
show that a large fraction of failures happen in bursts. (Section 4)
4. Quantify how likely a failure burst is associated with a given failure domain.
We find that most large bursts of failures are associated with rack- or multirack level events. (Section 4)
2. Nodes can become unavailable for a large number of reasons
1. For example, a storage node or networking switch can be overloaded;
a node binary or operating system may crash or restart;
a machine may experience a hardware error;
automated repair processes may temporarily remove disks or machines;
or the whole cluster could be brought down for maintenance
2. The vast majority of such unavailability events are transient
1. less than 10% of events last longer than 15 minutes
2. data is gathered from tens of Google storage cells, each with 1000 to 7000 nodes
3. GFS typically waits 15 minutes before commencing recovery of data
3. ARR is between 2% and 4% as reported in study [29]
Disk failures in the real world: what does an MTTF of 1,000,000 hours mean to you?
http://www.cs.toronto.edu/~bianca/papers/fast07.pdf
[19] also find 2% ~ 4%, but for some it can be 3.9% ~ 8.3%
3. Correlated failures is critical for availability
1. observed 37% of failures are part of a burst of at least 2 nodes
2. Two broad classes of failure bursts can be seen in the plot
1. a large number of failures in quick succession, e.g. a DC power outage
2. a smaller number of nodes failing at a slower rate at evenly spaced intervals, e.g. rolling upgrade
3. the paper defines a score, sum(ki * (ki - 1) / 2), ki is failure in i-th rack, to compare the rack concentration
and also the rack affinity score, 0.5 for random busrt, close to 1 for rack-correlated, close to 0 for anti-correlated
1. the finding is, larger failure bursts have higher rack affinity
all failures of 20+ nodes have rack affinity > 0.7, and 40+ nodes failure with > 0.9
4. for placement
1. rack-aware placemnet policy is better than uniform random placement
2. in general
1. placement deals with burst failure
2. network speed deals with long term reliability (repair needs to be faster than failures)
4. Markov model for stripe availability
1. Weibull has better fit for disk MTTF. but the exponential distribution is enough
2. correlated burst failures are added into the model,
i.e. failure events are independent of each other, but each event may involve multiple chunks
3. MTTF is calculated in standard method in [27] Adventures in stochastic processes
4. extend model to multi-cell (multi-DC)
1. treat each cell as a ‘chunk’ in the multi-cell ‘stripe’
5. findings
1. importance of recovery rate
1. with no correlated failures reducing recovery times by a factor of µ will increase stripe MTTF by a factor of µ^2 for R=3 and by µ^4 for RS(9, 4)
Reducing recovery times is effective when correlated failures are few
2. However, when correlated failures are taken into account, even a 90% reduction in recovery time results in only a 6% reduction in unavailability
2. failing to account for correlation of node failures typically results in overestimating availability by
at least two orders of magnitude and eight in the case of RS(8,4)
3. hardware failure rate
1. find that improvements below the node (server) layer of the storage stack do not significantly improve data availability
(latent disk error rate, disk failure rate)
2. On the other hand, cutting node failure rates by 10% can increase data availability by 18%
4. multi-cell
1. Replicating data across multiple cells (data centers) greatly improves availability because it protects against correlated failures
2. This introduces a tradeoff between higher replication in a single cell and the cost of inter-cell bandwidth
5. Some recommendations made by this framework in google
1. Determining the acceptable rate of successful transfers to battery power for individual machines upon a power outage
2. Focusing on reducing reboot times, because planned kernel upgrades are a major source of correlated failures
3. Moving towards a dynamic delay before initiating recoveries, based on failure classification and recent history of failures in the cell
11. Efficient Replica Maintenance for Distributed Storage Systems [2006, 295 refs]
http://www.cis.upenn.edu/~ahae/papers/carbonite.pdf
1. highlights
1. key ideas
1. durability algorithm must create replicas faster than permanent disk failures destroy it
2. increasing the number of replicas doesn't help a system tolerate a higher disk failure probability,
but does help tolerate bursts of failures
3. the equilibrium number of replicas: θ=µ/λf, i.e. replica creation rate / replica failure rate
if the system has more replicas, it cannot catch up to recover them. when
2. others
1. how to choose replica count, should 1) <= θ 2) tolerate large enough burst for acceptable MTTF
2. improve repair time: large node scope, i.e. how wide the node's replica are scattered.
however large scope increase monitoring load, and increase data loss possibility (more node-loss combinations turn into data loss)
3. reduce transient costs: reintegrate object replicas stored on nodes after transient failures
create replicas as needed, in batch
use timeouts, failures are consider transient before timeout
12. Reliability Mechanisms for Very Large Storage Systems [2003, 220 refs]
https://www.crss.ucsc.edu/Papers/xin-mss03.pdf
1. analyzing what reliability mechanism is enough for PB-level system.
2-way mirroring should be enough. 3-way mirroring or mirroring combined with RAID for high reliability.
1. this is not what today has. today its EB-level system 3-way mirroring and EC coding
2. there are fast recovery mechanisms proposed, they are already common today
13. When MTTDLs Are Not Good Enough: Providing Better Estimates of Disk Array Reliability [2008, 12 refs]
https://www.ssrc.ucsc.edu/Papers/paris-i2ts08.pdf
1. conventional MTTDL approach generally provides good estimates of the long-term reliability of repairable disk arrays,
but significantly underestimates their short-term reliability
2. proposed a technique reducing the margin of error by assuming that the disk array was replaced at frequent intervals
found same MTTDL approach provided fairly good estimates of the reliability of repairable redundant disk arrays as long as
the individual disk repair rate remained well above one thousand times the individual disk failure rate
3. how to evaluate the reliability of complex redundant disk arrays that are not promptly repaired within hours of a disk failure
The best alternative will be to turn to discrete simulation techniques
14. Reliability Challenges for Storing Exabytes
https://pdfs.semanticscholar.org/17e7/c943d15d9cc808393d0541f4c087bb18cefc.pdf
1. we consider only two causes for dataloss, namely full disk failure and latent disk errors
future also add losses due to operational errors, physical brick failure, losses due to networking outages, and generic catastrophes such as flooding
2. LSE (Latent Sector Errors) seem to be highly correlated
3. rather than a blind insistence on building using ever more reliable individual components,
we advocate the building f more reliable architectures that can inform reliable data placement based on the physical nature of the underlying infrastructure
4. Simply building exascale storage systems as a conglomeration of more reliable individual nodes will not scale
15. Mean time to meaningless: MTTDL, Markov models, and storage system reliability [2010, 61 refs]
https://www.usenix.org/legacy/event/hotstorage10/tech/full_papers/Greenan.pdf
1. MTTDL is meaningless
1. MTTDL literally measures the expected time to failure over an infinite interval.
This may make the MTTDL useful for quick, relative comparisons, but the absolute measurements are essentially meaningless
E.g. probablity of data loss for every year for the first 10 years of a system
2. Weibull distributions are more successful in modeling observed disk failure behavior, but we are using exponential distribution
3. Latent sector failures exhibit significant correlation both temporally and spatially within a device
Pareto distributions can best capture the burstiness of latent sector errors, as well as spatial and temporal correlations [11]
4. Disk repair activities such as rebuild and scrubbing tend to require some fixed minimal amount of time to complete
5. Memorylessness, Failure & Repair. aging is not considered.
and previous rebuilding is discarded after transited to new state
2. better matric, NOMDL: expected amount of data lost (in bytes) in a target system within mission time t
1. recommend to use Monte Carlo simulation to calculate NOMDLt
2. Many iterations of the simulator are required to get statistically meaningful results
---- Archival storage ----
16. Understanding Data Survivability in Archival Storage Systems [2012, 8 refs]
http://alumni.soe.ucsc.edu/~yanli/res/li-systor12.pdf
1. In most archival storage systems, data are replicated across several systems, sites, and backup media,
so the survivability of the data is based on the combined reliability of these storage
2. using Weibull reliability model
3. it's not using markov model, but Psurvival = 1 - Ploss1 * Ploss2 * ..
4. disk scrubbing is agreed to be an important feature for archival systems
5. leverage the S.M.A.R.T events: [23] found that a group of drives with Scan Errors are ten times more likely to fail
17. Disk Scrubbing in Large Archival Storage Systems [2004, 160 refs]
https://www.ssrc.ucsc.edu/Papers/schwarz-mascots04.pdf
1. it looks like very beginning paper of archival storge. it says to have proposed "data scrubbing"
2. disk MTTF uses 1.5E6 hours is AFR=8766/1.5E6=~0.5%, this is too low, should be AFR 2~4%
3. scrubbing disk techniques
1. scrub only when they are powered on
2. scrub by read data and compare with stored signature
3. power-on a disk lowers its reliability
16. Pergamum: Replacing Tape with Energy Efficient, Reliable, Disk-Based Archival Storage [2008, 176 refs]
https://www.usenix.org/legacy/event/fast08/tech/full_papers/storer/storer_html/
1. good reference as an archival storage.
2. highlights
1. compared to MAID (Massive Arrays of Idle Disks) who uses centralized controller,
Pergamum uses CPU per storage node. it relies on each CPU to be slow and power cheap.
it brings operational convenience that each storage node can be directly replaced.
2. Pergamum add NVRAM to each node, so that disk don't need to be powered up, and they can
do store signatures or compare them, defer writes, metadata requests.
the fundamental truth is NVRAM is more power cheap than power-on disks
3. Pergamum is able to keep 95% disks power-off in all time. This is the key to save energy.
1. I does worry about its sustaining write ingesting throughput,
which is important if we want to use it in cloud for customers along side blob/object storage
4. rebuild and data scrubbing are lazy, they try to only take place on powered on disks.
as author suggests, with intra-disk and inter-disk redundancy (e.g. (n+2)+2),
scrubbing once per year is enough for reliablity
5. data scrubbing use hash-tree signature to do comparison, thus save reads and data transmitted
6. deferred write, pass write delta, surrogate writes, needs only 2 disk active in same time per update.
7. data scrubbing also checks disk SMART status to choose target disks
---- Misc ----
17. Improving Disk Array Reliability Through Expedited Scrubbing [2010, 11 refs]
https://www.ssrc.ucsc.edu/Papers/paris-nas10.pdf
1. on RAID-6, we propose to start an urgent scrubbing scan whenever we detect a failure of one of the array disks
18. Efficiently Identifying Working Sets in Block I/O Streams [2011, 21 refs]
https://www.ssrc.ucsc.edu/Papers/wildani-systor11.pdf
1. place physical protocol analyzer on storage bus, group by calculating distance, support multiple application accessing.
distance is computed from time diff and file offset diff. next use kNN clustering or graph clique covering to determine groups.
---- Erasure coding ----
19. In Search of I/O-Optimal Recovery from Disk Failures [2011, 45 refs]
https://www.usenix.org/conference/hotstorage11/search-io-optimal-recovery-disk-failures
1. good, this paper finds the code to minimize recovery IO at given fault tolerance sacrificing storage overhead
propose a new code, using only XOR, each paritiy covers two data symbols.
in each failure case how to recovery needs to be calcuated a priori
the recovery strategy calculating is an NP-hard problem,
the paper uses a tree graph for it, graph depth equals to number of failures.
basically it is enumeration search of using all recovery equation combinations, and use Dijkstra's algorithm to find shortest path
2. the code is based on Flat XOR code
"We solve the problem of determining how to recalculate the lost data
while minimizing the total number of surviving bits that are read"
3. there is a fundamental trade-off between recovery IO vs storage overhead at a given fault tolerance
1. MDS minimize storage overhead
2. this code gives mimize IO cost
3. In between these extrema, lie codes that increase storage overhead and reduce recovery I/O,
such as GRID/Weaver code
4. it's like an extreme LRC with only overlaping local parities, and don't need GF multiply coefficients
1. not sure how it compares with MBR regenerating code, though the latter tends to increase IO count but has less network traffic.
and MBR regenerating code also does brings more storage overhead
-- 20171011 --
20. Rethinking Erasure Codes for Cloud File Systems: Minimizing I/O for Recovery and Degraded Reads [2012, 235 refs]
https://www.usenix.org/conference/fast12/rethinking-erasure-codes-cloud-file-systems-minimizing-io-recovery-and-degraded
0. good paper to read. first part of the paper is the algorithm to find optimal recovery scheduling for less symbols
next the method is used for degraded read, to reduce io, by merge user-read symbols into recovery-needed symbols
next it proposed rotated reed solomon code, like the RDP, rotation makes recovery equations easier to be lucky to cover user-read symbols,
and for disk rebuild, like RDP optimal recovery, we can use two parities for one disk failure to reduce IO
however, in later LRC papers such as Pyramid Codes, authors think rotated RS code saving 20-30% is inferior than LRC
1. highlights
1. the paper follows "In Search of I/O-Optimal Recovery from Disk Failures" with same authors
2. the related works and backgrond introduction is good. it covers most codec works and tells their core features
2. related work
1. previous simpler work: "In Search of I/O-Optimal Recovery from Disk Failures"
2. as referenced in LRC paper later, they said LRC is better in saving IOs
1. "The savings of these schemes are typically around 20%-30% [Khan et al. 2011, 2012; Xiang et al. 2010], much less than pyramid codes."
Pyramid codes: https://staff.ie.cuhk.edu.hk/~mhchen/papers/pyramid.ToS.13.pdf
3. it's like ChengH team is continuously working on EC codec to reduce IO
21. The RAID-6 Liber8tion Codes [2008, 182 refs]
https://www.usenix.org/legacy/event/fast08/tech/full_papers/plank/plank_html/
1. Liber8tion is frequently referenced in other papers for compare. It has good recovery properties as reducing 30% IO (said in "Rethinking .." paper).
The name is for the freedom of constructing RAID-6 codes. Liber8tion code is defined on Coding Distribution Matrix (CDM), see 3.3.
It uses only XOR. It achieves lower bound of number of 1's in matrix. It is MDS code. It even outperforms RDP codes in some parameters.
The paper uses "bit matrix scheduling" to find the optimal recover equations for a failure, thus reduce XOR count.
the schedules can be precalculated and cached (since it tolerates 2 disk failure at most)
2. highlights
1. the related works & background part is good, as it summarized typical codes for RAID-6
RS code -> Parity Array: EVENODD -> RDP. X-Code however doesn't fit RAID-6 specification;
STAR code is for than two failures, it boils down to EVENODD still
22. STAR: An Efficient Coding Scheme for Correcting Triple Storage Node Failures [2005, 233 refs]
https://www.usenix.org/legacy/event/fast05/tech/full_papers/huang/huang.pdf
1. STAR is modified EVENODD code that tolerate 3 disk failures. it is MDS.
Recovery achieves lower bound of 3 XORs per symbol. (EVENODD up to 10 XORs)
2. highlights
1. STAR uses p+3 columns, first 2 parity columns are same with EVENODD.
the 3rd parity column is slop -1 rather than slop 1 of EVENODD 2nd parity
2. decoding steps are illustrated in section 4.
after finding a start point, there can be multiple crosses choosen
---- Coding theory ----
23. Optimizing Galois Field Arithmetic for Diverse Processor Architectures and Applications [2008, 53 refs]
http://www.kaymgee.com/Kevin_Greenan/Publications_files/greenan-mascots08.pdf
1. composite field technique, agnostic to hardware. GF(2^l) => GF(2^n = 2^l^k), so that large field 2^32 is reducted to 2^8 or smaller
pinning entire lookup table in cache help improve performance. and there are many evaluation and observation experiences
and, application-specific optimizations for composite fields can further improve performance (figure 4(d))
the related works section tells more about GF operation implementation works and status
2. existing table lookup methods for GF mul and optimizations
1. log/antilog lookup table needs O(n) space. but needs to 3 table lookup for a multiply
2. left-right table, breaks multiplier into left & right part, and lookup in two smaller tables, left-table and right-table
3. more table lookup optimizations, see table 1
24. Jerasure: A Library in C/C++ Facilitating Erasure Coding for Storage Applications - Version 1.2 [2007, 271 refs]
https://web.eecs.utk.edu/~plank/plank/papers/CS-08-627.pdf
1. the famous EC library that Ceph is using. For Jerasure 1.2, it adds Blaum-Roth and Liber8tion codes.
it has many codec implementations, can be used for the RAID ones and cloud storage CauchyRS/MDS codes
the code word w is typically 8, 16, 32
---- Erasure coding ----
25. EVENODD: An Efficient Scheme for Tolerating Double Disk Failures in RAID Architectures [1995, 682 refs]
https://authors.library.caltech.edu/29320/1/BLAieeetc95a.pdf
1. very classic, very old. many new codes are based on EVENODD. like STAR, RDP, liber8tion, etc.
basically it gave us the first different and good code from RS.
EVENODD tolerates 2 disk failures, uses only XOR, achieves MDS, and has good encode/recovery performance.
The two parity column of it provides horizontal redundancy and diagonal redundancy
2. related materials
1. "The RAID-6 Liber8tion Codes" has introduction to EVENODD code
26. Rebuilding for Array Codes in Distributed Storage Systems [2010, 73 refs]
https://arxiv.org/abs/1009.3291
1. improved version of EVENODD code to minimize recovery IO. To build one data node erasure, only 3/4 information symbols need to be transimitted.
it borrowed some idea from regenerating code [8], to calculate middle block and transimit it instead of transimit whole data
2. materials
1. referenced in "In Search of I/O-Optimal Recovery from Disk Failures" as the EVENODD code
27. Self-repairing Homomorphic Codes for Distributed Storage Systems [2010, 190 refs]
https://arxiv.org/pdf/1008.0064.pdf
1. interesting paper. together with "On the locality of codeword symbols", "Simple Regenerating Code", this paper first introduced "locality" to codecs.
self-repairing codes: not systematic, not MDS, lost parities can reconstruct from a subset of fixed number-ed other parities.
the code construction is Homomorphic SRC: encode needs mul but recover only needs XOR;
it uses interesting polynominal operations and p(a+b) = p(a) + p(b). an parity can be obtained as a linear combination of other parities
2. related materials
1. Coding Techniques for Distributed Storage Systems (by Fr´ed´erique Oggier)
http://phdopen.mimuw.edu.pl/lato12/LectPoland.pdf
1. this is almost the same material of content with F.Oggier's long survey "Coding Techniques for Repairability in Networked Distributed Storage Systems"
but it tells more detail about Self-repairing Homomorphic Codes
2. in chapter 1, there is actually very good intro to Galois Field
28. Locally Repairable Codes [2012, 280 refs]
https://arxiv.org/abs/1206.3804
1. very good paper. authored by D. S. Papailiopoulos, together with F.Oragger, P. Gopalan, ChengH, they proposed the "locality" in EC codecs
"On the Locality of Codeword Symbols" prooves that, when each node has entropy a=M/k (or say data size), recoverability bound d<=n-k-roof(n/r)+2
this paper allows a=(1+e)M/k, allow sacrificing storage ovhead, to maximize reliability, for given locality r: d<=n-roof(k/(1+e))-roof(k/(r(1+e)))+2
the analysis method is based on network information flow graph and entropy.
the paper then popose explict code constructs, it is actually the "Simple Regenerating Code", it is MDS and has great local repair ability
locality can be set to sub-linear of k, r=log(k), r=sqrt(k), to vanish the storage space penalty as k grows large
2. so, to summarize
1. LRC code achieves locality lower bound with best recoverability without sacrificing space overhead
2. Simple Regenerating Code achieves locality lower bound with best recoverability when allow sacrificing space overhead
3. r can be configured to other sub-linear functions of k, e.g. r=log(k), r=sqrt(k),
to construct non-trivial locality codes for large k with small storage overhead penalty
29. A Practical Analysis of Low-Density Parity-Check Erasure Codes for Wide-Area Storage Applications [2004, 110 refs]
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.133.5556&rep=rep1&type=pdf
1. good papers that tell many LDPC characteristics. it walkthrough all LDPC code constructs and generation method and measure their characteristics.
2. highlights
1. performance panelty is determined by overhead factor f. only when code length almost > 50, LDPC starts to vastly outperform RS code
the f decreases as code length grows, dropping to nearly 1.00 as n grows to 100,000+
2. the storage space overhead can be 1/3, 1/2, 2/3. it's not need to be ~2x.
3. the bipartite graph edges are generated by probability distribution, this is basically how different LDPC varies
regular graphs, i.e. nodes have constant in/out degree, cannot achieve "channel capacity" asymptotically
4. the performance in theory is asymptotic value, in real case, you need to run generation methods multiple times to get one good construction
some generation method may require long time to find a good construction
---------
[Update 20180305]
1. readings: remaining piled up papers
1. Clay Codes: Moulding MDS Codes to Yield an MSR Code
https://www.usenix.org/conference/fast18/presentation/vajha
1. Very good paper. Awesome work.
"Clay codes extend the theoretical construction presented by Ye & Barg with practical considerations from a coupled-layer perspective that leads directly to implementation"
Clay Code solved almost every drawback in regenerating code existing for years. "Clay codes provide the first practical implementation of an MSR code"
1. Clay Code is MSR regenerating code. And it allows low storage overhead. This is not like Product-Matrix code which requires n > 2k-2
2. It's array code, and the sub-packetization level, i.e. array size, is small enough
3. It can regenerate multiple node failure with reduced traffic. This is hardpoint for regenerating code for many years
1. the MSR property illustrated is for 1 node failure. multi-node it's "reduced traffic", bound given by appendix
4. The Clay Code is based on RS code, actually pretty simple and easy transform
2. how the code works
1. the author only gives an example construct of (4,2) code. it's a bit lazy, because
0. how could you write so little for such an awesome code construct that solved almost every problem in regenerating code?
1. there is no generalized code construct, e.g. how to assign the x, y, z correctly
2. there is no illustration of how to regenerate multiple node failure with reduced traffic
1. yes, there is, see appendix. and there is repair algorithm listed. this answers the general code construct and decoding method
3. there is no math proof of the code property and the theory bounds
4. In Table 1 it’s said Clay Code has polynomial sub-packetization level.
But in the "(n = qt, k, d) (α = q^t ,β = q^(t−1))" given later in paper, α is exponential to n. It’s confusing.
2. The baseline plain RS code. multiple packets abstracted as layers
Then we add in the "Pairs" across layers. Encode "pairs" again with a simple inversible matrix
For decode, we start from intersection score from 1 to biggest. using the pair PRT -> MDS Decode -> PFT to decode layer by layer.
1. there is no general code construct except the very simple example (4,2) code. I've been gussing the general construct
1. Coordinates x is 0~q-1, y is 0~t-1, z is (0~q-1, 0~q-1, .., 0~q-1) {t times}.
1. Yes, this is it. See appendix. They are there
2. The "pair" follows same way described in paper. In each fixed y, z, ranging through all x, there is one and only one unpaired point
3. the decode and selecting correct layers are complicated ..
1. In appendix, there is repair algorithm listed. now we have all we need.
3. in the evaluation part
1. the charts mostly shows "d=n-1". for regenerating code to reduce total IO count, this is not enough
2. the (14,10,11~13) network traffic and disk-read charts compared to RS are not reaching theory numbers
3. other highlights
1. Sub-chunking through interleaving: pack the bytes in same position in code array together, to form the subchunk
1. in implementation part, the calculation is performed in unit of sub-chunk, rather than directly every byte
2. "Locally repairable codes such as the Windows Azure Code [15] and Xorbas [28] trade the MDS property to allow efficient node-repair by accessing a smaller number of helper nodes"
3. "Clay codes possess all of the desirable properties mentioned above, and also offer several additional advantages compared to the Ye-Barg code"
4. "Clay codes can be constructed using any scalar MDS code as building blocks"
5. "The savings in repair bandwidth of the Clay code arises from the fact that parity-check constraints are judiciously spread across layers of the C data cube"
6. to extend Clay Code for any (n,k,d) where not q divide n, the paper uses the imaginary data node whose data is all zero
1. "The technique used is called shortening in the coding theory literature"
7. "The helper nodes are to be chosen in such a way that if a y-section contains a failed node, then all the surviving nodes in that y-section must act as helper nodes"
"If no such choice of helper nodes is available then it is not a repairable failure pattern"
n. related materials
1. [29] XORing Elephants: Novel Erasure Codes for Big Data [2013, 418 refs]
http://www.vldb.org/pvldb/vol6/p325-sathiamoorthy.pdf
1. facebook datacenter has employed (10,4) RS code.
this paper is also by facebook. Locally Repairable Codes (LRCs) based on RS (10,4). t HDFS-Xorbas
1. achievements: a 2x reduction in disk I/O and repair network traffic.
the disadvantage of the new code is that it requires 14% more storage
compared to RS code
2. geo-distribution is key futhure direction to improving latency and reliability
RS code is be impractical due to high bandwidth requirements
local repairs make it possible
2. "Locally Repairable Codes", share the same authors with this paper: Dimitris S. Papailiopoulos, Alexandros G. Dimakis
https://arxiv.org/abs/1206.3804
3. the code construct here
1. "The basic idea of LRCs is very simple: we make repair efficient by adding additional local parities"
1. I'd say this is exactly the same with Azure LRC code ..
2. HDFS-Xorbas computes two extra parities for a total of 16 blocks per stripe (10 data blocks, 4 RS parities and 2 Local XOR parities)
1. Note that it's XOR.
4. the new local parities are calculated by MapReduce and in a incremental manner.
1. the code design makes new code rollout well adopted
2. [35] Explicit Constructions of Optimal-Access MDS Codes With Nearly Optimal Sub-Packetization [2017, 34 refs]
https://pdfs.semanticscholar.org/75d9/fedfa0c13b983e315ec2460da0c2e6d85775.pdf
1. the "optimal access" property and the "group optimal access" property
Create an Issue or comment below