Time-series Learning Algorithms Candidates
The time-series algorithms once selected and evaluated to build a analyzing and self-learning system for Openstack application awareness. OPs are always collecting bunches of metrics which are essentially time-series.
Fourier Transform (FT)
What it can do
- Decompose f(t) to combination of basic waves (sine/cosine).
- Smoothing.
- Test periodicity
- i.e. Largest cycle period from FFT is significantly smaller than data span.
- Forecasting and modeling, if time-series is periodic.
Summary
- Transform f(t), which is on t time domain, to F(w), which is on w frequency domain. F(w) = f(t)’s component on frequency w.
- FT transforms time-series f(t) into a sum of sine/cosine.
- FT is invertible, i.e. a FT decomposition of sine/cosine waves is unique.
- Suitable for periodic functions. Non-periodic functions result in non-constant F(w) or infinite sum of since/cosine.
- Discrete Fourier Transform (DFT) is used for discrete computer sampling, with time complexity O(n*n).
- Fast Fourier Transform (FFT) is the faster version approximation of DFT, with time complexity O(n*log(n)).
- Do FFT multiple times for better smoothing, according to Netflix Scryer.
Theory
Euler’s formula demonstrates the basic connection between complex numbers and triangular functions.
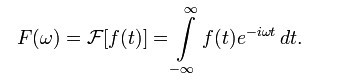
How F(w) is calculated? e^iwt = cos(wt) + isin(wt), which is one of f(t)’s wave component. f(t)*e^iwt test f’s correlation with e^iwt. The bigger correlation, the bigger coefficient, which is F(w), results in.
!8394323_1298253739kqo6.jpg!
To reverse F(w) to f(t), we simply add each wave component together. A wave component is e^iwt, the cos(wt) + isin(wt), multiply its coefficient F(w).
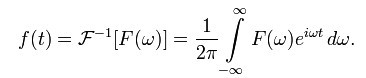
How FFT is used for smoothing? “FFT Filter smoothing is accomplished by removing Fourier components with frequencies higher than a cutoff frequency”, according to here. Also cutoff amplitude can be used. Choose the threshold wisely.
References
- Theory Explanation
- Wiki FT
- Wiki Frequency Spectrum
- Wiki Fourier Series
- FT Animation
- FT and Epicycle
- FFT Implementation
- FFT Smoothing and Comparison
- Netflix Scryer Use FFT for Forecasting
Moving Average (MA)
What it can do
- Smoothing for long-term trends.
- To see long-term trends.
Summary
- Replace the current point with the (weighted) average of it and nearby range.
- Moving average smoothed curve usually fits the originally one badly, but become useful to see long-term trends. This is different from FFT smoothing.
Theory
Simple moving average (SMA) is the unweighted mean of the previous n data.
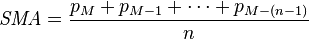
| Exponential moving average (EMA), or exponential smoothing ([wiki | http://en.wikipedia.org/wiki/Exponential_smoothing]), gives weighted average from current point to beginning, where the weight for each older point decreases exponentially. |
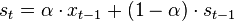
There are yet many other moving average algorithms.
References
ARIMA (Autoregressive Integrated Moving Average)
What it can do
- Time-series data modeling and forecasting.
- Trends, circulation, seasonality is taken cared.
Summary
- Seen from random process (statistics) perspective, rather than wave.
- Time-series is considered as random process of autoregressive model + moving-average model, or informally a random-trend + random-walk.
- Random-trend is recognized by differencing, i.e. y(i) - y(i-1), the autoregressive model.
- Random-walk is recognized by moving-average model.
- Parameters:
- p is the number of autoregressive terms,
- d is the number of nonseasonal differences, and
- q is the number of lagged forecast errors in the prediction equation.
- Autocorrelation is used to determine lag factor p & q.
- A bit complex.
- Very widely used in forecasting, such as marketing data, stock trends.
Theory
Given ARMA(p’ ,q) model:
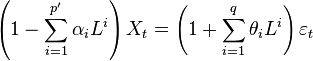
Assume the left side polynomial has a unitary root of multiplicity d
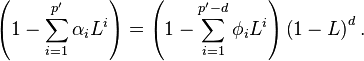
ARIMA(p,d,q) process expresses it with p=p’−d
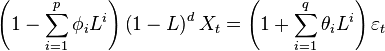
Above are random process models.
Reference
- Introduction to ARIMA - nonseasonal models
- Time-series Forecasting Methods
- ARIMA Basic and Use
- Wiki
- Texts - ARIMA models
Classical Decomposition
What it can do
- Decompose time-series into trend+seasonal+remainder
Summary
- Not recommended now
- Essentially use Moving Average (MA)
Theory
Step 1
- Calculate trend-cycle component = N-MA(series), or trend = 2×N-MA(series)
Step 2
- Calculate the detrended series: s2 = series - trend
Step 3
- Taking month March as an example, seasonal index is the average of all the March values in s2. Then adjust seasonal index so that they adds to zero. seasonal component = seasonal index stringed together.
Step 4
- Remainder component = series - trend - season component.
Reference
X-12-ARIMA Decomposition
What it can do
- ARIMA based time-series decomposition
Summary
- A sophisticated method
- Employs ARIMA
- There is currently no R package for X-12-ARIMA decomposition
References
STL Decomposition
What it can do
- Time-series decomposition
Summary
- Equipped in R.
- Advantages over the classical decomposition method and X-12-ARIMA.
- Only provides additive decompositions.
- Parameters: trend window & seasonal window
References
More
- Triangular fitting?
- Autocorrelation may be relevant to cycle finding
Neuron Network
What it can do
- Time-series modeling and forecasting
Summary
- Use neuron network model for time=series
- Previous N points are used as input for the model
- Equipped in R.
- Magically it works.
- Has seasonal models.
Theory
Neuron network model, with previous N points in time-series as input to the model.
References
ACF & PACF
What it can do
- Residual diagnostics
- The reminder component of time-series should contain no pattern. Use these tests for it.
- Detect seasonality, according to here
Summary
- ACF, autocorrelation function, is used to test reminder
- Also “Average Test / Durbin-Watson Test” can be used for same purpose
- Small p-value of Durbin-Watson Test indicates significant autocorrelation remaining.
Theory
Average of reminder component, if no pattern remaining, should be zero.
ACF or autocorrelation of reminder component, if no pattern remaining, should show not significant spike or lag.
References
- OTexts Residual diagnostics: [https://www.otexts.org/fpp/5/4]
Augmented Linear Regression (Netflix Scryer)
What it can do
- Accurate forecasting
Summary
- The more you know about your pattern, the better forecasting algorithm you can make.
- Especially repeated cycles
- Must have and exploit the pattern that
- the cycle of day repeats
- the cycle of week repeats
- Accurate and very simple.
References
- Netflix Scryer Part1: [http://techblog.netflix.com/2013/11/scryer-netflixs-predictive-auto-scaling.html]
- Netflix Scryer Part2: [http://techblog.netflix.com/2013/12/scryer-netflixs-predictive-auto-scaling.html]
Periodogram
What it can do
- To detect any periodicities/seasonality
Summary
- Periodogram is the basic modulus-squared of the Fourier transform.
- Essentially same with Power Spectral Density, categorized in “spectral analysis”
- The squared radius of epicycle.
- It is graphical technique, which usually requires manual inspection.
-
Other seasonality detection [methods http://www.itl.nist.gov/div898/handbook/pmc/section4/pmc443.htm], which are also graphical techniques: - A run sequence plot will often show seasonality.
- A seasonal subseries plot is a specialized technique for showing seasonality.
- Multiple box plots can be used as an alternative to the seasonal subseries plot to detect seasonality.
- The autocorrelation plot can help identify seasonality.
Theory
First, remember the Fourier Transform decompose time-series Xn into
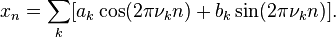
v represents the frequency.
Periodogram is a graph/function with v as abscissa (horizontal axis), and ordinates (vertical axis) as:
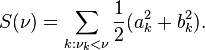
I don’t remember whether the coefficient “1/2” is correct, but periodogram does show “the basic modulus-squared of the Fourier transform”. Remember fourier transform in complex format, the sin(..) part is “i*sin(..)”.
But, it is NOT finished yet. Basic periodogram has “Leakage Problem” and maturer methods are derived from this: refer to [http://www.statsoft.com/Textbook/Time-Series-Analysis#problem].
References
- Identify Patterns in Time Series Data: [http://www.statsoft.com/Textbook/Time-Series-Analysis#spectrum]
- What method can be used to detect seasonality in data?: [http://stats.stackexchange.com/questions/16117/what-method-can-be-used-to-detect-seasonality-in-data]
- Spectral density estimation: [http://en.wikipedia.org/wiki/Spectral_estimation]
- Spectral density: [http://en.wikipedia.org/wiki/Power_spectrum]
- Periodogram: [http://en.wikipedia.org/wiki/Periodogram]
My Crafted Spike Detection
What it can do
- Spike/peak detection
Summary
- Use standard deviation to detect outliers.
- Peak outliers are taken as spikes.
- Neighbor spike points which are not significantly different are merged.
Theory
Step 1: De-trend. Remove trend component from the original time-series.
Step 2: Identifier outliers, who’s |value-mean| >= a*standard_deviation. The “a” is a changeable parameter, usually 3.
- Sometime it is useful to omit Step 2 by setting a to 0.
Step 3: Select from outliers, who is larger/smaller than its neighbor on both sides. Call them S points.
Step 4: Merge two S points A & B, if
- A & B are both above/below mean, and
- points between A & B are all outliers of same side to mean, but not S point, and
- NOT (at least one point X between A & B, min(|A.value-X.value|, |B.value-X.value|) is larger than threshold k). k is a changeable parameter. i.e. a gap exists between A & B.
A, B is merged to whom is farther from mean.
Step 5: Merge all S points pair satisfy Step 4’s condition.
The remaining S points are spikes.
- There are yet more methods for searching spike/peak points.* For example, find maxima points who is larger than left and right neighbor points within distance k. Refer to [Simple Algorithms for Peak Detection in Time-Series]
References
- Simple way to algorithmically identify a spike in recorded errors: [http://stats.stackexchange.com/questions/41145/simple-way-to-algorithmically-identify-a-spike-in-recorded-errors]
- Detecting steps in time series: [http://stats.stackexchange.com/questions/20612/detecting-steps-in-time-series]
- Simple Algorithms for Peak Detection in Time-Series: [http://www.tcs-trddc.com/trddc_website/pdf/SRL/Palshikar_SAPDTS_2009.pdf]
- How to find local peaks/valleys in a series of data?: [http://stats.stackexchange.com/questions/22974/how-to-find-local-peaks-valleys-in-a-series-of-data]
- Detecting cycle maxima (peaks) in noisy time series (In R?): [http://stackoverflow.com/questions/16341717/detecting-cycle-maxima-peaks-in-noisy-time-series-in-r]
- Peak detection of measured signal: [http://stackoverflow.com/questions/3260/peak-detection-of-measured-signal]
Dynamic Time Wrap
What it can do
- Calculate similarity of two time series.
Summary
- Get similarity of the whole time series, not subsequence.
- Can take time series of different length (N, M).
- Tolerate accelerations and decelerations, refer to here
- Very costly, cpu NM, mem NM. Cause R Studio to stuck
- But, there exist faster versions. See here.
- Cannot tolerate that: one time series’s Y value is shifted by C, or scaled by S
- R package: “dtw”
Theory
For two points x and y, d(x, y) is a distance between the symbols, e.g. d(x, y) = | x - y |. Pseudo-code as below:
int DTWDistance(s: array [1..n], t: array [1..m]) {
DTW := array [0..n, 0..m]
for i := 1 to n
DTW[i, 0] := infinity
for i := 1 to m
DTW[0, i] := infinity
DTW[0, 0] := 0
for i := 1 to n
for j := 1 to m
cost:= d(s[i], t[j])
DTW[i, j] := cost + minimum(DTW[i-1, j ], // insertion
DTW[i , j-1], // deletion
DTW[i-1, j-1]) // match
return DTW[n, m]
}
References
- Wiki: [http://en.wikipedia.org/wiki/Dynamic_time_warping]
- Time Series Analysis and Mining with R: [http://rdatamining.wordpress.com/2011/08/23/time-series-analysis-and-mining-with-r/]
- R Archive: [http://dtw.r-forge.r-project.org/]
Pearson Correlation
What it can do
- Time series similarity
Summary
- Fast, simple, widely used.
- Tolerate Y axis shift or scaled.
- R equipped in ccf()
- Cannot tolerate that: time series A and B have different length.
- You have to scale the X axis before hand (interpolation).
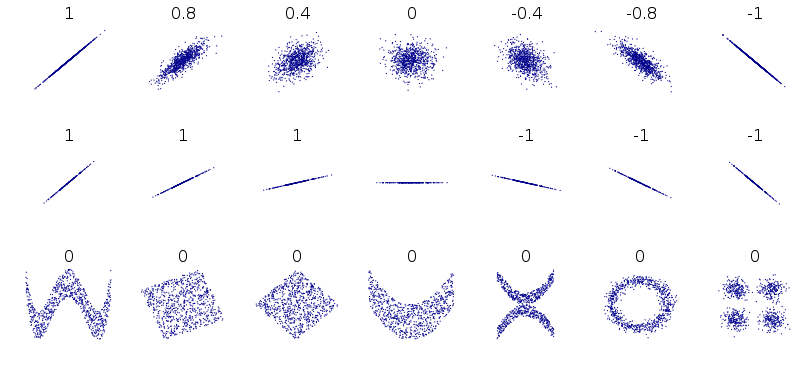
- Be careful with the Y=C case, or Y=X=C. See below chart.
Theory
Time series X=X(t), Y=Y(t). Think X, Y similar as Y=k*X+C. Then Y=Y(X) must be linear regressionable if they are similar. Pearson correlation is right what is used to determine linear relation fitness.
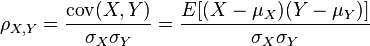
Demonstrate chart of Pearson correlation examples:
References
- Time series similarity measures: [http://quant.stackexchange.com/questions/848/time-series-similarity-measures]
- Wiki: [http://en.wikipedia.org/wiki/Pearson_correlation_coefficient]
- R has ccf(): [http://stats.stackexchange.com/questions/23993/how-to-correlate-two-time-series-with-possible-time-differences]
Linear Segmentation
What it can do
- Segment time-series into segments, separated by point of change.
Summary
- In R package ‘ifultools’.
- Has really poor result, with or without noise.
- Doesn’t necessarily detect extreme points.
- Piecewise linear segmentation of a time series
- Cool method but why so bad result?
- More segmentation methods can be found in References below.
Theory
Use a sliding window of length n, each time move one point forward. If the least square regression of the window, has changed angle exceeding angle.tolerance, current point is marked as segmentation boundary.
References
- LinearSegmentation: [http://cran.r-project.org/web/packages/ifultools/ifultools.pdf]
- Segmenting Time Series: A Survey and Novel Approach: [http://www.ics.uci.edu/~pazzani/Publications/survey.pdf]
- R ‘segmented’ package: [http://cran.r-project.org/web/packages/segmented/index.html]** It has ‘segmented()’ to do piecewise linear regression, but need breakpoints as parameter.
- R ‘changepoint’ package: [http://cran.r-project.org/web/packages/changepoint/index.html]** It has changepoint detection based on mean and variance.
- R ‘strucchange’ package: [http://cran.r-project.org/web/packages/strucchange/index.html]** It has sophisticated breakpoint detection but seems no that kind of breakpoint I want.
- R ‘breakpoint’ package: [http://cran.r-project.org/web/packages/breakpoint/breakpoint.pdf]** It uses cross-entropy, but the result seems not what I need.
- Wiki time-series segmentation: [http://en.wikipedia.org/wiki/Time-series_segmentation]
- Wiki change point detection: [http://en.wikipedia.org/wiki/Change_detection]
My Crafted Time-Series Segmentation
What it can do
- Time-series segmentation
- Provide basic pattern fragments for recognition
Summary
- FLAWS: when left/right regression walk across a maxima point, result is wrong
- Use linear regression on both side of a point to determine
- Time complexity O(N*C), N is time series length, C is a constant.
- Detects extreme points.
- Better perform smoothing (FFT or others) before use this method.
Theory
Given a point, calculate the least square regression within K points of left side and right side, noted as Ll and Lr.
If the angles of Ll and Lr differs more than threshold G, current point is a segment boundary point.
References
- Segmenting Time Series: A Survey and Novel Approach: [http://www.ics.uci.edu/~pazzani/Publications/survey.pdf]
- LinearSegmentation: [http://cran.r-project.org/web/packages/ifultools/ifultools.pdf]
My Crafted Find Minima
What it can do
- Find minima points.
- Can be modified to find maxima points.
- Then can find spike points.
- As input of time-series segmentation
Summary
- Find minima points by comparing left and right neighbor average.
Theory
Step 1: find minima points by comparing left & right neighbor points’ average.
Step 2: merge minima points that are too close.
R Code:
neighbor_minima = function(x, k, t=0){
res = c(1)
for(i in 1:length(x)){
l1 = max(1, i-k)
l2 = max(1, i-1)
r1 = min(i+1, length(x))
r2 = min(i+k, length(x))
lmean = mean(x[l1:l2])
rmean = mean(x[r1:r2])
cur = x[i]
if(cur-lmean<t&&cur-rmean<t){
res = append(res, i)
}
}
res = append(res, length(x))
merged = TRUE
while(merged){
merged = FALSE
res_merge = c()
for(i in 1:(length(res))){
if(i>=2&&res[i-1]-res[i]>-k){
if(x[res[i-1]]<=x[res[i]]){
merged = TRUE
next
}
}
if(i<=length(res)-1&&res[i+1]-res[i]<k){
if(x[res[i+1]]<=x[res[i]]){
merged = TRUE
next
}
}
res_merge = append(res_merge, res[i])
}
res = res_merge
}
res_merge
}
References
- Find local maxima and minima: [http://stackoverflow.com/questions/6836409/finding-local-maxima-and-minima]
- Finding local extrema: [http://stats.stackexchange.com/questions/30750/finding-local-extrema-of-a-density-function-using-splines]
Apriori + Pattern Search Tree
What it can do
- Find pattern in time-series
- Pattern means: repeated segment with high occurrence frequency
- Can only detect EXACTLY matched segment
Summary
- Apriori algorithm
- Tree data structure + pruning
- Only finds EXACTLY matched pattern
- Could be slow/mem-consuming on large series.
Theory
The classic Apriori algorithm.
See page 5 in Discovering Similar Patterns in Time Series
Reference
- Discovering Similar Patterns in Time Series P5: [ftp://ftp.cse.buffalo.edu/users/azhang/disc/disc01/cd1/out/papers/kdd/p497-caraca-valente.pdf]
Apriori + Pattern Search Tree + Distance Similar
What it can do
- Find pattern time-series
- Similar segment can be found
Summary
- Modified from “Apriori + Pattern Search Tree”
- Use distance measure on similarity instead of exactly match
- Problem: if A & B are to be resulted similar, subsequence of A and B from left to right must be all similar, to avoid A/B being pruned.
- Could be slow/mem-consuming on large series.
Theory
See page 6 in Discovering Similar Patterns in Time Series
References
- Discovering Similar Patterns in Time Series P5: [ftp://ftp.cse.buffalo.edu/users/azhang/disc/disc01/cd1/out/papers/kdd/p497-caraca-valente.pdf]
My Crafted Pattern Recognition
What it can do
- Find pattern in time-series, i.e. the repeating segments.
Summary
- Find similarity on segmentations.
Theory
First, do segmentation on time-series.
- You need to choose a segmentation algorithm from above.
Second, cluster the segments using similarity measure.
- You need to choose a similarity measure algorithm from above.
Now high occurrence segments are obtained, they are patterns.
References
- Pattern Recognition and Classification for Multivariate Time Series: [http://www.dai-labor.de/fileadmin/Files/Publikationen/Buchdatei/tsa.pdf]. Like mine, find similarity on time-series segmentations
- A good discussion on time-series segmentation
- Good material
Linear Interpolation
What it can do
- Fill points in time-series
Summary
- I can use it to change irregular time interval to regular one
- R way is cumbersome and fragile. I recommend use Python to implement it.
- Be careful with two NA point next to each other
Theory
Draw a straight line from NA point’s left and right neighbor. NA point’s y value is taken from the line.
R implementation seems to be cumbersome and fragile. I prefer to user Python to do it.
mdf=read.csv('~/Desktop/workspace/WLAP-cloud-intelligence/study/ceilometer_dump/2014-8-5/cpu_util.csv')
#mdf$time2 = as.POSIXct(mdf$time, origin="1970-01-01") # get the time string from timestamp, the mdf$time is lost somehow
#x1=xts(mdf$value, mdf$time2) # xts requires using Date for time, but zoo is enough
z1=zoo(mdf$value, mdf$time)
z2=zoo(NA, end(z1)+seq(-length(z1)+1, 0)*30) # the empty "slots"
z3=merge(z2,z1)
#z4=na.locf(z3) # use value of prior point for NA
# use linear interpolation for NA, but this WON'T work if two NA next to each other
# this is really frigle. so, I'd better implement myself interpolation in python
z4=na.approx(z3[,2], na.rm=FALSE, rule=2)
z5=merge(z2, z4, all=FALSE) # intersection of z2, z4
# z6 is the result
z6=z5[,2]
Reference
- Zoo tutorial: [http://cran.r-project.org/web/packages/zoo/vignettes/zoo-quickref.pdf]
- An example of merge: [http://www.climatescience.cam.ac.uk/community/blog/view/667/interpolation-of-time-series-data-in-r]
- Time in millisecond to zoo: [http://stackoverflow.com/questions/11494188/zoo-objects-and-millisecond-timestamps]
- Some time-series CRAN: [http://cran.r-project.org/web/views/TimeSeries.html]
- Irregular time-series: [http://stackoverflow.com/questions/12623027/how-to-analyse-irregular-time-series-in-r]
- Creating regular from irregular: [http://stackoverflow.com/questions/10423551/creating-regular-15-minute-time-series-from-irregular-time-series]
- Linear interpolation: [http://en.wikipedia.org/wiki/Linear_interpolation]
UCR Suite
What it can do
- Compare time series similarity in DTW (Dynamic Time Warp)
Summary
- A DTW algorithm even faster than ED (Euclidean Distance)
Theory
Refer to reference 1, optimizations including
- Using the Squared Distance
- Lower Bounding
- Early Abandoning of ED and LB_Keogh
- Early Abandoning of DTW
- Exploiting Multicores
And
- Early Abandoning Z-Normalization
- Reordering Early Abandoning
- Reversing the Query/Data Role in LB_Keogh
- Cascading Lower Bounds
Reference
- Searching and Mining Trillions of Time Series Subsequences under Dynamic Time Warping: [http://www.cs.ucr.edu/~eamonn/SIGKDD_trillion.pdf]
- UCR Suite site: [http://www.cs.ucr.edu/~eamonn/UCRsuite.html]
Motifs Discovery
What it can do
- Discovery motifs (the repeated subsequence in time-series)
Approaches
-
Online Discovery and Maintenance of Time Series Motifs: [http://www.cs.ucr.edu/~eamonn/online_motifs.pdf]
- Gives online approach
-
A disk-aware algorithm for time series motif discovery: [http://link.springer.com/article/10.1007%2Fs10618-010-0176-8]
- Gives offline on disk approach
-
SAX (Symbolic Aggregate approXimation): [http://homepages.abdn.ac.uk/yaji.sripada/pages/teaching/CS4031/information/SAX.pdf]
- Transform a time-series in to a string with arbitrary length, using an alphabet. Brief description at [https://code.google.com/p/jmotif/wiki/SAX]** Official site: [http://www.cs.ucr.edu/~eamonn/SAX.htm]
- The authors are right who first proposed “Motifs Discovery” in [http://cs.gmu.edu/~jessica/Lin_motif.pdf]
- JMotif - motif discovery in java with SAX: [https://code.google.com/p/jmotif/]
Tip & Tricks
-
For smoothing, we usually iterate a smoothing algorithm multiple times (e.g. 3x), to achieve better effect.
-
“We might subtract the trend pattern from the data values to get a better look at seasonality” in here
-
Moving Average usually give middle point greater weight, in order to mitigate the smoothing effect.
-
Summarize of data smoothing techniques: [http://wweb.uta.edu/faculty/ricard/Classes/KINE-5350/Data%20Smoothing%20and%20Filtering.ppt]
-
Selecting different MA order results in different trends obtained. “In particular, a 2×12-MA can be used to estimate the trend-cycle of monthly data and a 7-MA can be used to estimate the trend-cycle of daily data. Other choices for the order of the MA will usually result in trend-cycle estimates being contaminated by the seasonality in the data.” (from [https://www.otexts.org/fpp/6/2])
-
After the day/month seasonality is extracted, you can use STL on remainder, with very small seasonal window to extract remaining periodicity.
Create an Issue or comment below