Dig the Math in RDP Optimal Recovery

RDP (row-diagonal parity) code is a popular code. It is of n+2, one parity encodes horizontal strips, and one for diagonal (slightly different from EVENODD). It tolerates 2 disk failure. Optimal Recovery of Single Disk Failure in RDP Code Storage Systems proposed the optimal recovery scheduling, which achieves mimimum disk IO count and balanced recovery workload across disks.

In this post I try to understand the math in the paper and also the thinking behind. The pasted paper page images (at tail of this post) are annotated with key steps. When exploring this RDP optimal recovery problem, I think

• Pick a few specific p=5 or p=7 example to try out a few recovery combinations first, may help realize that there are minimal read conditions
• Use Python etc programming to simulate, may help find that each minimal reads conditions have equal number of reads

Then it’s the power of math representation. Not necessary for any high-level math, but just the good math representation, and some analytical skill, helped solve the puzzle of minimal read

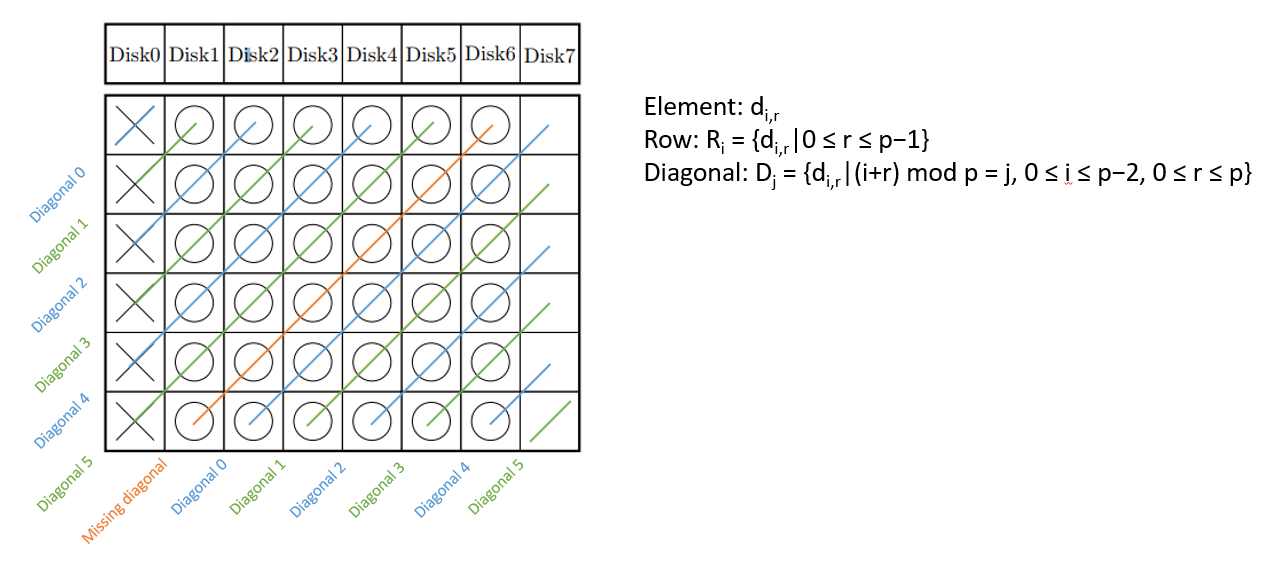
• First we math represents each element, then each row, then each diagonal
• Next, we math represents the intersect point of row and diagnoal. That’s the overlapping read. More overlapped read, are we closer to minimal read
• A recovery strategy can be represented as an array of [0 to p-2], each slot with 0 or 1 for recover by row and recover by diagonal
• The key for minimal read is that, each row and diagonal has one and exactly one cross point, i.e. overlap
• So we can list the math equation to final read count now, or instinctively know that row count should equal to diagonal count used for recovery

Next, we come to the problem of getting balanced read on top of minimum read.

• It’s a dare think to believe minimum read and balanced read can be achieved together. I think a few construction trial, and probably program enumeration can help
• At this stage, possibly, if we stop doing more math. Brutal force math search should also help we find any optimal construction. Good computation power can always make up the short of analytical math. Now we mapreduce/spark stuff. I guess it also indicates why HPC and supercomputer is important to top science.
• The paper did use math to represent how many elements from a disk is read. The formula is not really hard, as long as we represent the recovery strategy as 01 sequence, which makes it calculatable.
• We could have stopped here. With the exact math condition formulas, we can just brutal force search for all optimal constructs. But the paper goes further, which shows the beauty and uniform of math.
• The magic part is to use multiplicity set to understand the math formula of condition (3), the key requirement to achieve balanced read.
• The further magic math is, using combinatorics or group theory, the multiplicity set can be constructed in common way, thus the nonzero square set.
• So, in the end, not only we got the math constraint formula to provide balanced and minimual read. We also get the multiplicity set solution to easily construct them.

As in most part, it’s not deep math, but the good math representation, and analytical skills to use them and find good cut-in point, are the key parts to solve the problem.

Here’s the schema of how RDP (Row-Diagonal Parity) encode its rows and diagonals. The diagonal encoding has uniformed representation.

Here’s the annotated paper page shots.