Understanding NP-Complete

Definitions

We define the symbols in this section to prepare for explaining NP-complete.

1. f(x): f is the problem. E.g. in the given graph G, list the SHORTEST-PATH beween V1 and V2. x is the input for this problem. E.g. the graph G and V1, V2. Usually, f(x) can be an optimization problem.

2. C(f(x)) -> {0, 1}: NP theory discusses only decision problem, i.e. a problem which outputs only yes or no (1 or 0). So we need C to transform f(x) into a decision problem. For example, the SHORTEST-PATH problem can be transform into: “Does there exists a path in graph G connecting V1 and V2, which is shorter than length k?” Once f(x) is solved, C(f(x)) is solved; so f(x) is harder than C(f(x)) (problem reduction). C(f(x)) is the NP problem we gonna discuss here. Note that by definition, an NP problem C doesn’t necessarily need an f(x).

3. A(x, y): f(x) says “find something”. C(f(x)) says “does the something exist?”. We name the “something” here as y. y is called certificate in NP theory. According to the denifition of NP, C(f(x)) should be verifiable in polynomial time. We name its verification algorithm as A(x, y) here. A(x, y) says: given the “something” y, does it really satisfy what C(f(x)) wants? A(x, y) has polynomial time complexity. Finally the NP problem C(f(x)) can be seen as “does a y that satisfies A(x, y) exist?”

What is NP-complete

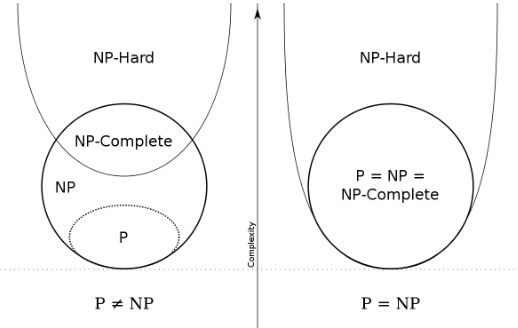
A decision problem C is NP-complete if

1. C is a NP problem, and

2. C is equal or harder than any other NP problems (“hardness” is defined by problem reduction)

The first NP-complete problem is the circuit satisfiability problem. To prove rule 2 for it

1. Every NP problem C has its A(x, y)

2. Since A(x, y) is an algorithm of polynomial time complexity, we can construct its equivalent combinational logic circuit

3. If there exists an y satisfying A(x, y), the equivalent y must satisfy our circuit, vice versa. The later one is the circuit satisfiability problem.

4. So, if circuit satisfiability problem is solved, we know whether y exists, thus solving C. This means circuit satisfiability problem is equal or harder than any other NP problem.

An NP-complete problem is the hardest problem in NP set. The true magic is that, later people found many other problems are no less harder than the circuit satisfiability problem (proved by problem reduction, see below); i.e. they are off the same hardness. So the truth of NP-complete set is that

1. NP-complete problems are the hardest in the NP set

2. There are many NP-complete problems, and they are of the same hardness.

To prove a NP-complete problem

The NP problem to prove is C1, which has verification algorithm A1(x, y). The general approach is to

1. Find an existing NP-complete problem C2 and its A2(x, y).

2. Given the A2(x, y), construct its equivalent A1(x, y). So that if any y satisfies A1(x, y), it satisfies A2(x, y), and vice versa. This is the reduction.

3. So that if we could solve C1, i.e. to know whether a y satisfying A1(x, y) exists, we solve C2. It means C1 is no less harder than C2, thus C1 is NP-complete.

For more about NP-complete, refer to wiki or “Introduction of Algorithms”.